70+ Quadratic Equation Most Repeated Questions for IBPS Clerk 2025 Exam

The IBPS Clerk 2025 exam is one of the most competitive banking exams in India. Every year, lakhs of candidates appear for this exam to secure clerical positions in public sector banks. Out of the three major sections of the Prelims exam, the Quantitative Aptitude section plays an important role in determining your overall performance. In Quant, one of the most scoring topics is Quadratic Equations. For the past 10 years, Quadratic Equations have been a constant feature in the IBPS Clerk Prelims exam, making it a must-have topic for candidates looking to gain accuracy and speed.

Free IBPS Clerk Reasoning, Quant and English Most Asked Question Set

What are Quadratic Equations in IBPS Clerk Exam?

A Quadratic Equation is a polynomial equation of the form:

ax² + bx + c = 0

Here, a, b, and c are constants, x is the variable, and a ≠ 0. The solutions, or roots, of the equation represent the values of x that satisfy it. In the RRB PO exam, quadratic equation questions often involve comparing the roots of two equations (involving variables x and y) to determine their relationship, such as:

• x > y
• x < y
• x = y
• x ≥ y
• x ≤ y

A relationship cannot be established

Importance of Quadratic Equations in IBPS Clerk 2025

Quadratic equations are considered one of the fastest-to-solve topics in Quantitative Aptitude. Unlike lengthy topics such as Data Interpretation or Arithmetic Word Problems, quadratic equations can be solved in just 10–20 seconds per question with the right approach.

• Weightage: Usually, 5 questions are asked in the Prelims exam.
• Difficulty Level: Easy to Moderate.
• Scoring Nature: If you know the method, it’s 100% accuracy guaranteed.
• Time Management: Solving 5 questions in less than 3 minutes boosts your overall attempts.

Thus, mastering quadratic equations is essential if you aim to score 25+ marks in Quant Prelims.

Concepts You Must Know Before Solving

A quadratic equation is of the form:

ax² + bx + c = 0 (where a ≠ 0)

Methods to Solve Quadratic Equations

1. Factorisation Method – Splitting the middle term to find factors.
2. Quadratic Formula –

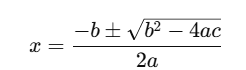
1. Comparison of Roots – For IBPS, direct root comparison between two equations (x and y).
2. Sign of Roots – Positive/negative checking helps in quicker elimination.

70+ Quadratic Equations IBPS Clerk Most Repeated Questions

Here, we provide 70+ most important quadratic equation questions that have been repeatedly asked in IBPS Clerk exams and mock tests. These are divided into sets of 10 questions each for easy practice.

Question 1: In the question, two equations I and II are given. You have to solve both equations to establish the correct relation between x and y and choose the correct option.

I. 3x² – 24x + 36 = 0

II. 4y² = y + 5

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 2: In the question, two equations I and II are given. You have to solve both equations to establish the correct relation between x and y and choose the correct option.

I. x² – 2x – 63 = 0

II. y² + 14y + 48 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 3: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² + 15x + 54 = 0

II. y² + 20y + 99 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 4: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. 3x + 7y = 53

II. 7x – 5y = 17

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 5: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² – 27x + 180 = 0

II. y² – 24y + 140 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 6: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² – 11x + 30 = 0

II. y² – 11y + 18 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 7: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² + 3x – 10 = 0

II. y² – 5y + 6 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 8: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² – 5x + 4 = 0

II. y² + 2y – 3 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 9: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. 3x + 5y = 21

II. 9x – 2y = 12

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 10: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. 4x² + 16x – 20 = 0

II. 2y² + 11y – 6 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

How to Solve Quadratic Equation Question for IBPS Clerk 2025 Exam

Here we are providing three steps to solve a quadratic equation for the IBPS Clerk 2025 exam. Candidates must follow these steps and boost your perforamance.

Step 1: Factorise the Equation

• Break the middle term (coefficient of xxx) into two numbers whose product = (first coefficient × last coefficient).
• Example: x2+5x+6=0x^2 + 5x + 6 = 0x2+5x+6=0 Middle term = 5, factors of 6 = 2 and 3
  So, roots = -2, -3

Step 2: Find the Roots of Both Equations

• Solve both quadratic equations separately.
• Example:
  Equation I: x2+5x+6=0⇒x=−2,−3x^2 + 5x + 6 = 0 \Rightarrow x = -2, -3×2+5x+6=0⇒x=−2,−3
  Equation II: y2+7y+10=0⇒y=−2,−5y^2 + 7y + 10 = 0 \Rightarrow y = -2, -5y2+7y+10=0⇒y=−2,−5

Step 3: Compare the Roots

• Compare each root of xxx with each root of yyy.
• Example:
  x=−2,−3x = -2, -3x=−2,−3 and y=−2,−5y = -2, -5y=−2,−5
  • When x=−2x = -2x=−2, compare with yyy: (-2 = -2), (-2 > -5)
  • When x=−3x = -3x=−3, compare with yyy: (-3 < -2), (-3 > -5)

Since the relationship is mixed, the answer is: (e) Relationship cannot be established

Conclusion

Quadratic Equations are undoubtedly one of the easiest and most repeated topics in the IBPS Clerk 2025 Exam. By mastering this topic, you’re not only ensuring full marks in one part of the exam but also saving crucial time for tougher sections like DI and Arithmetic.

Join our exclusive Telegram group where our experts are ready to answer all your queries, guide you in banking exam preparation, and give personalised tips to boost your success. Get access to real-time solutions, expert advice, and valuable resources to improve your study journey.

Other Related Blogs  

Quadratic Equation for IBPS Clerk FAQ

• Sign Up on Practicemock for Updated Current Affairs, Topic Tests and Mini Mocks
• Sign Up Here to Download Free Study Material