Master Permutation and Combination Tips for RBI Grade B Exam

Permutation and Combination is an important topic in the Quantitative Aptitude section of the RBI Grade B Phase 1 exam. These questions test candidates’ ability to count possible arrangements or selections in different situations. They are based on basic counting principles, logic, and sometimes probability. The past exam analysis tells, Permutation and Combination questions usually carry 1 to 2 marks in the Quants section, which carries a total of 30 marks. The difficulty level of this part is moderate for most candidates. This means they can be solved in under 50 seconds if you know the right method or solving techniques. That gives you extra time for lengthy questions like Data Interpretation or complex arithmetic problems. In this article, we’ll discuss the basics, formulas, patterns, and easy tricks to solve Permutation and Combination questions quickly and accurately.

ALSO READ: How to Score Maximum Marks in Cloze Test

Common Types of Permutation and Combination Questions

The main difference between Permutation and Combination is that in Permutation, repetition or the order of things matter, but in Combination, they don’t. So, it’s important to know the types of them. 

If you check RBI Grade B past papers, these are the main types you will see:

Simple Permutations

Here, you are asked to arrange objects in a certain order. Example: How many ways can the letters of the word “BANK” be arranged? These are the most basic and are quick to solve with factorials.

Permutations having Repetition

Some objects repeat. This reduces the number of arrangements.

Example: How many different words can be formed from “LETTER”?

Here, you divide by the factorial of each repeated letter count.

Restricted Permutations

Here, certain conditions are given.

Example: In how many ways can 5 people stand so that two specific people always stand together?

These require grouping and then arranging.

Simple Combinations

Here, you select items without considering the order.

Example: From 10 players, choose 3 for a team.

Formula:

Combinations with Restrictions

Some selections are not allowed or must follow a rule.

Example: From 8 candidates, choose 4, but two friends cannot be together in the selection.

These need careful case-wise counting.

Mixed Problems

These combine arrangements and selections.

For example: Select 3 students from the given 5, and then arrange them in a row.

These need both formulas below in one problem:

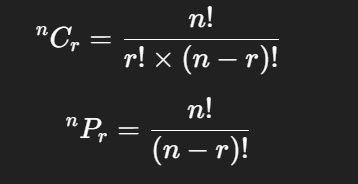
ALSO READ: How to Score Maximum Marks in Cloze Test & Ratio & Proportion Concepts and Shortcuts for RBI Grade B Exam

5 Important Formulas to Remember

There are a few formulas you must remember:

1. Factorial Rule

n!=n×(n−1)×(n−2)…3×2×1n! = n \times (n-1) \times (n-2) \dots 3 \times 2 \times 1

For example: 4!=244! = 24

2. Permutation Formula

Number of arrangements of rr items from nn items:

• n! means multiply all numbers from 1 to n (total items)
• / means  divide by
• p! Means multiply all numbers from 1 to p (items of 1st kind)
• × means times
• q! means multiply all numbers from 1 to q (items of 2nd kind)
• × means times
• r! … means same for other kinds of items

Meaning: total arrangements when some items repeat.

3. Combination Formula

Number of selections of rr items from nn items:

4. Permutations with Repetition

When some items look the same:

5. Principle of Fundamental Counting

If one task can be done in m ways and another in n ways, total ways = m × n.

Tips to Solve Permutation and Combination Quickly

Here’s the approach that works in the exam:

1. Write the Given Data Clearly: List out n and r first. Identify if it’s arrangement or selection.

2. Decide Between P and C Early: If the order matters, use permutation. If not, use combination.

3. Break Down Restrictions: If conditions are given, think in cases before applying formulas.

4. Use the Principle of Fundamental Counting: For step-by-step tasks, multiply the ways for each step.

5. Avoid Long Factorial Calculations: Cancel terms before multiplying to save time.

Types of Questions Asked in RBI Grade B Phase 1 Exam

Given below are the types of Permutation and Combination

Example 1: Simple Permutation

How many different 4-digit numbers can be formed from the digits 1, 2, 3, 4 without repetition?

Number of ways = 

Answer: 24 numbers.

Example 2: Permutation with Restriction

In how many ways can the letters of “BANK” be arranged so that B and A are always together?

Treat BA as one unit → units = BA, N, K = 3 units.
Arrangements = 3!=63! = 6
BA can be AB as well, so multiply by 2 → Total = 12 ways.

Answer: 12 arrangements.

Example 3: Simple Combination

From 8 students, choose 3 for a project.

Number of ways = 

Answer: 56 ways.

Example 4: Combination with Restriction

From 8 candidates, choose 3, but two specific candidates cannot be together.

Total ways without restriction = 8C3=56^8C_3 = 56

Ways with both together: Treat them as 1 unit → select 1 more from 6 → 6C1=6^6C_1 = 6 ways.

Within the pair, they can be arranged in 1 way (since order doesn’t matter in selection).

So restricted ways = 6.

Allowed ways = 56 − 6 = 50 ways.

Answer: 50 ways.

Shortcuts and Tricks You Must Know

Given below are the most important shortcuts that you must know to quickly solve all types of Permutation and Combination:

• Find Order Early: Decide if it’s permutation or combination before solving.
• Cancel Factorials: Saves time and avoids large multiplications.
• Group Method: Use grouping for “together” or “separate” conditions.
• Complementary Counting: Sometimes it’s faster to count the total and subtract restricted cases.
• Step Method: Break complex problems into smaller steps using the Fundamental Principle.

How to Practise Effectively

Daily practice is the only way to make this topic quick in the exam.

• Daily Drills: Solve 10 permutation/combination problems every day.
• Review of Past Paper: Look at 7 years’ RBI Grade B Quant papers for patterns.
• RBI Garde B Phase 1 Mock Tests: Train to solve under 50 seconds per question.
• Self-Created Problems: Create your own small cases. It makes understanding deeper.

Mini Task for You

Try solving these questions below quickly:

1. How many arrangements of the letters in “SUCCESS” are possible?
2. In how many ways can a president, vice-president, and secretary be chosen from 8 members?

Sample Questions for Practice

Now, it’s time to practice the types of questions that you can face in the real exam. Go through all the questions below and try to solve them on your own. Compare your answers with the ANSWER KEYS and SOLUTIONS given under these questions.

Question 1: From a group of 8 men and 6 women, a committee of 8 persons is to be selected. Find the number of ways in which the committee can be formed with at-least 5 men in the group.

A) 1572

B) 1577

C) 1569

D) 1589

E) None of these

Question 2: Find total number of ways in which the word “UNCHATACTERISTICALLY” can be arranged so all the vowels always come together.

A) 13190 × 11!

B) 12740 × 11!

C) 12180 × 11!

D) 17910 × 11!

E) None of these

Question 3: The sum of all the possible numbers of four digits formed by digits 2, 3, 4 and 5 using each digit once is:

A) 94424

B) 99657

C) 93324

D) 94367

E) None of these

Question 4: How many four letter words having at most three consonants and at least 1 vowel can be formed by using the letters of the word “CASTLIEY”?

A) 65

B) 360

C) 720

D) 1560

E) None of these

Question 5: How many words with or without meaning can be formed by using all the letters of the words “PRACTICE” such that all the vowels always occupy even positions?

A) 240

B) 720

C) 1440

D) 2880

E) None of these

प्रश्न 1: 8 पुरुष और 6 महिला के एक समूह से, 8 व्यक्तियों के एक समिति का चयन किया जाता है|कम से कम 5 पुरुष के साथ समिति का चयन कितने तरीके से किया जाता है?

A) 1572

B) 1577

C) 1569

D) 1589

E) None of these

प्रश्न 2: उन तरीकों की कुल संख्या ज्ञात करें जिनमें शब्द “UNCHATACTERISTICALLY” को व्यवस्थित किया जा सकता है ताकि सभी vowels हमेशा एक साथ आ सकें।

A) 13190 × 11!

B) 12740 × 11!

C) 12180 × 11!

D) 17910 × 11!

E) None of these

प्रश्न 3: प्रत्येक अंक का एक बार प्रयोग करके अंक 2, 3, 4 और 5 से बनने वाली चार अंकों की सभी संभावित संख्याओं का योग है:

A) 94424

B) 99657

C) 93324

D) 94367

E) None of these

प्रश्न 4: शब्द “CASTLIEY” के अक्षरों का उपयोग कर ऐसे कितने 4 अक्षरों के शब्द का निर्माण किया जा सकता है जिसमे अधिकतम तीन consonants और कम से कम 1 vowel हो?

A) 65

B) 360

C) 720

D) 1560

E) None of these

ANSWER KEYS and SOLUTIONS:

Solution 1: 4)

Desired number of ways = (⁸C₅ × ⁶C₃) + (⁸C₆ × ⁶C₂) + (⁸C₇ × ⁶C₁) + ⁸C₈ = 1120 + 420 + 48 + 1 = 1589

Hence, option d.

Solution 2: 2)

Desired number of ways {7!/(3! × 2!)} × {14!/(3! × 3! × 2!)} = 12740 × 11!

Hence, option b.

Solution 3: 3)

Total number of different numbers of 4 digits formed using these digits only once = 4! = 24

The number formed whose unit digit is ‘2’ = 6

The number formed whose unit digit is ‘3’ = 6

The number formed whose unit digit is ‘4’ = 6

The number formed whose unit digit is ‘5’ = 6

Sum of the total number of unit digits = 2 × 6 + 3 × 6 + 4 × 6 + 5 × 6 = 84

Desired sum = 84 + 84 × 10 + 84 × 100 + 84 × 1000 = 84 × (1000 + 100 + 10 + 1) = 84 × 1111 = 93324

Hence, option c.

Solution 4: 4)

There are 5 consonants and 3 vowels in the word “CASTLIEY”

Case I: 1 vowel and 3 consonants are there in the word

Number of ways of selecting letters = ³C₁ × ⁵C₃ = 3 × 10 = 30

Case II: 2 vowels and 2 consonants are there in the word

Number of ways of selecting letters = ³C₂ × ⁵C₂ = 3 × 10 = 30

Case III: 3 vowels and 1 consonant are there in the word

Number of ways of selecting letters = ³C₃ × ⁵C₁ = 1 × 5 = 5

So the total number of ways in which the letter are selected = 30 + 30 + 5 = 65

These 4 letters can be arranged with in the word in 4! = 24 ways

So the total number of words formed = 24 × 65 = 1560

Hence, option d.

Solution 5: 3)

There are 4 even positions and 3 vowels.

Number of ways of filling these 3 vowels = ⁴P₃ = 24

Number of ways of filling 5 consonants = 5!/2! = 60

So, the total number of words formed = 60 × 24 = 1440

Hence, option c.

ALSO READ: Word Swap Tricks for RBI Grade B Phase 1 Exam

Are you preparing for the RBI Grade B exam 2025? If so, it’s the ideal time to start and accelerate your exam preparation. The notification can be released anytime soon!

Start preparing with the course that best suits you below!

Takeaway

Permutation and Combination is a scoring topic in the Quant section of the RBI Grade B exam if you master the basic formulas and shortcuts. Once you get comfortable, you can solve these questions in seconds. Make them a fixed part of your daily Quant practice, and you will secure these marks quickly in the real exam.

• Sign Up on Practicemock for Updated Current Affairs, Topic Tests and Mini Mocks
• Sign Up Here to Download Free Study Material