80+ Most Asked Quadratic Equation Questions for LIC AAO 2025 Exam

Quadratic Equations are one of the most important topics in the Quantitative Aptitude section of the LIC AAO 2025 exam. Typically, the Prelims exam contains 5 to 6 questions from this topic, making it crucial for aspirants to have a clear understanding and strategy. In this article, we will provide detailed knowledge of quadratic equations, including the basic concepts, methods of solving, types of questions asked in previous LIC AAO exams, and the most commonly asked questions with step-by-step solutions. By going through this article, candidates can strengthen their conceptual understanding, learn shortcut methods, and practice effectively to attempt all quadratic equation questions with confidence and accuracy in the exam.

Quadratic equations are not just about solving standard problems; they also appear in the form of word problems, inequalities, and comparisons of roots. This article aims to cover everything from basics to advanced techniques to ensure that you are fully prepared for the LIC AAO 2025 exam.

Understand Quadratic Equations

A quadratic equation is a second-degree polynomial equation in a single variable, typically expressed as:

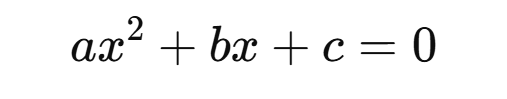
where aaa, bbb, and ccc are constants, and a≠0a \neq 0a=0. The solutions to this equation are known as the roots, which can be found using methods such as factoring, completing the square, or the quadratic formula:

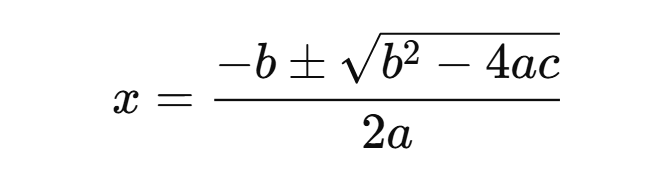
In the LIC AAO exam, quadratic equations are often presented in the form of inequalities or comparisons between two equations.

80+ Most Asked Quadratic Equation Questions PDF Link

For aspirants aiming to ace the LIC AAO 2025 exam, practising a wide variety of questions is key. To help you prepare effectively, we have compiled 80+ Most Asked Quadratic Equation Questions with detailed solutions in a handy PDF. This resource covers all important question types, including factorisation the quadratic formula. Download the PDF and start practising to improve your speed and accuracy in the exam.

Question 1: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x²+ 9x –52 = 0

II. y²+19y –66 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 2: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x³ = 1331

II. y²–26y + 168 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 3: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. 3x – 2y = 31

II. x + 3y = 69

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 4: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x²+ 21x +90 = 0

II. y²+25y + 114 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 5: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. 2x²= 392

II. y²–29y + 210 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 6: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² – 7x + 12 = 0

II. y² – 20y + 75 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 7: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² + 11x + 30 = 0

II. y² + 19y + 90 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 8: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² – 22x + 120 = 0

II. y² – 26y + 165 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 9: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I.x² + 23x + 120 = 0

II.y² – 4y – 96 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

Question 10: In the question, two equations I and II are given. You have to solve both the equations to establish the correct relation between x and y and choose the correct option.

I. x² – 10x – 119 = 0

II. y² + 21y + 108 = 0

A) x > y

B) x < y

C) x = y or the relationship cannot be established

D) x ≥ y

E) x ≤ y

ANSWER KEYS and SOLUTIONS:

Solution 1: C)

From I:

x²+ 9x –52 = 0

x²+ 13x – 4x–52 = 0

x(x + 13) – 4(x +13) = 0

(x + 13) (x – 4) = 0

x = -13, 4

From II:

y²+19y – 66 = 0

y²+22y – 3y – 66 = 0

y(y + 22) – 3(y + 22) = 0

(y + 22) (y – 3) = 0

y = -22, 3

So, no relation can be established between x and y.

Hence, option c.

Solution 2: B)

From I:

x³ = 1331

x = 11

From II:

y²–26y + 168 = 0

y²–12y – 14y + 168 = 0

y(y – 12) – 14(y – 12) = 0

(y – 12) (y – 14) = 0

y = 12, 14

So, x < y.

Hence, option b.

Solution 3: A)

From I:

3x – 2y = 31

3x = 31 + 2y

x = (31 + 2y)/3 …..(1)

From II:

x + 3y = 69

(31 + 2y)/3 + 3y = 69

31 + 2y + 9y = 69 × 3

31 + 11y = 207

11y = 207 – 31

11y = 176

y = 16

Put the value of ‘y’ in equation (1)

x = (31 + 2 × 16)/3

= (31 + 32)/3

= 63/3 = 21

So, x > y.

Hence, option a.

Solution 4: C)

From I:

x²+ 21x +90 = 0

x²+ 15x + 6x +90 = 0

x(x + 15) + 6(x +15) = 0

(x + 15) (x + 6) = 0

x = -15, -6

From II:

y²+25y + 114 = 0

y²+19y + 6y + 114 = 0

y(y + 19) + 6(y + 19) = 0

(y + 19) (y + 6) = 0

y = -19, -6

So, no relation can be established between x and y.

Hence, option c.

Solution 5: E)

From I:

2x²= 392

x²= 196

x = ± 14

From II:

y²–29y + 210 = 0

y²–14y – 15y + 210 = 0

y(y –14) – 15(y – 14) = 0

(y –14) (y – 15) = 0

y = 14,15

So, x ≤ y.

Hence, option e.

Solution 6: B)

From I:

x²– 7x + 12 = 0

x² – 4x – 3x + 12 = 0

x(x – 4) – 3(x – 4) = 0

(x – 4)(x – 3) = 0

x = 4,3

From II:

y² – 20y + 75 = 0

y² – 15y – 5y + 75 = 0

y(y – 15) – 5(y – 15) = 0

(y – 15)(y – 5) = 0

y = 15, 5

Hence, option b.

Solution 7: A)

From I:

x² + 11x + 30 = 0

x² + 6x + 5x + 30 = 0

x(x + 6) + 5(x + 6) = 0

(x + 6)(x + 5) = 0

x = -6, -5

From II:

y² + 19y + 90 = 0

y² + 10y + 9y + 90 = 0

y(y + 10) + 9(y + 10) = 0

(y + 10)(y + 9) = 0

y = -10, – 9

Hence, option a.

Solution 8: C)

From I:

x²– 22x + 120 = 0

x²– 12x – 10x + 120 = 0

x(x – 12) – 10(x – 12) = 0

(x – 12)(x – 10) = 0

x = 12, 10

From II:

y²– 26y + 165 = 0

y²– 11y – 15y + 165 = 0

y(y – 11) – 15(y – 11) = 0

(y – 11)(y – 15) = 0

y = 11, 15

Hence, option c.

Solution 9: E)

From I:

x² + 23x + 120 = 0

x² + 8x + 15x + 120 = 0

x(x + 8) + 15(x + 8) = 0

(x + 8)(x + 15) = 0

x = -8, -15

From II:

y² – 4y – 96 = 0

y² – 12y + 8y – 96 = 0

y(y – 12) + 8(y – 12) = 0

(y – 12)(y + 8) = 0

y = 12, -8

Hence, option e.

Solution 10: A)

From I:

x²– 10x– 119 = 0

x² + 7x – 17x – 119 = 0

x(x + 7) – 17(x + 7) = 0

(x + 7)(x – 17) = 0

x = -7, 17

From II:

y²+ 21y + 108 = 0

y²+ 12y + 9y + 108 = 0

y(y + 12) + 9(y + 12) = 0

(y +12)(y + 9) = 0

y = -9, -12

Hence, option a.

For More Questions, Download the PDF

80+ Most Asked Quadratic Equation Questions PDF Link

How to Solve Quadratic Equations Easily

Mastering quadratic equations is all about understanding the methods and practising smartly. Here’s a step-by-step approach to solving them efficiently for the LIC AAO exam:

1. Solve by Factoring (Master Factorisation)

Factoring is usually the fastest way to solve quadratic equations in exams.

Example:
x² – 5x + 6 = 0

• Find two numbers whose product is 6 (constant) and sum is -5 (coefficient of x).
  
• Numbers are -2 and -3.
  

Split the middle term:
x² – 2x – 3x + 6 = 0

Factorise:
(x – 2)(x – 3) = 0

Roots: x = 2, 3

Tip: Memorise common factor pairs for numbers up to 100. This will save time in exams.

2. Use the Quadratic Formula Wisely

For equations that don’t factorise easily, use:
x = [-b ± √(b² – 4ac)] / (2a)

• Calculate the discriminant (b² – 4ac) carefully.
  
• It tells you whether the roots are real, equal, or complex.
  
• Practice square roots of common numbers mentally (√144 = 12, √169 = 13) to save time.

3. Use the Table Method for Comparing Roots

When comparing roots of two equations, a simple table method helps you organise your calculations quickly.

Example:
Equation: 40x² – 47x + 12 = 0

• Split the middle term using the sum and product of roots.
• Divide by the coefficient of x² to get roots: x = 4/5, x = 3/8

Repeat the same steps for the second equation and then compare the roots. This makes comparison problems much easier.

4. Practice Previous Year Papers

Going through the last 5 years of LIC AAO or RRB PO papers is extremely helpful.

• Most quadratic questions follow a pattern with slight variations in coefficients.
• You’ll get an idea of which types of questions appear most frequently (factorable, inequalities, sum/product of roots, word problems).
  It also helps you understand difficulty levels and the time required per question.

5. Take Topic Tests

Daily practice with topic-focused tests can drastically improve your speed and accuracy.

• Start with easy questions, then gradually move to moderate and difficult ones.
• Aim: solve 15-20 quadratic questions per day to build confidence and strengthen weak areas.

6. Take Mini and Sectional Mock Tests

If you feel weak in the Quant section, do mini mock tests or sectional tests.

• Focus on the Quant section for 30–45 minutes, simulating exam conditions.
• Identify mistakes, revise concepts, and track improvement.
• This method ensures you are consistently improving in weak areas without feeling overwhelmed.
  

7. Take Full-Length Mock Tests

Full-length mocks help you understand your overall performance.

• Simulate the real exam with time limits and all sections.
• It trains you to manage time between sections and maintain accuracy.
• Helps build stamina and reduces exam-day stress.

Disclaimer: The quadratic equation questions, solutions, and strategies provided are compiled from expert references and exam trends. They are intended for practice and guidance only, not official LIC AAO exam content. Actual exam questions may differ. Candidates should always verify details through official LIC notices before relying on them.

Join our exclusive Telegram group where our experts are ready to answer all your queries, guide you in banking exam preparation, and give personalised tips to boost your success. Get access to real-time solutions, expert advice, and valuable resources to improve your study journey.

• Sign Up on Practicemock for Updated Current Affairs, Topic Tests and Mini Mocks
• Sign Up Here to Download Free Study Material